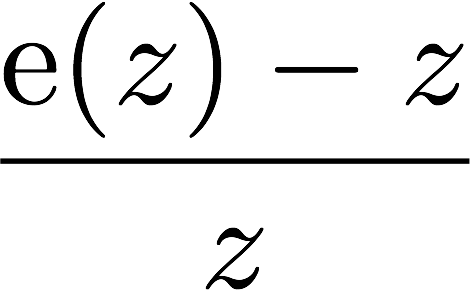A selection of scientific computing projects that I maintain on GitHub.
pychebfun
An implementation of Trefethen and Battles' Chebfun package in Python.
bsplinelab
Using the de Casteljau algorithm to create $C^2$ splines on symmetric spaces.
diffeopt
Minimise any loss function using automatic differentiation to do direct or indirect matching
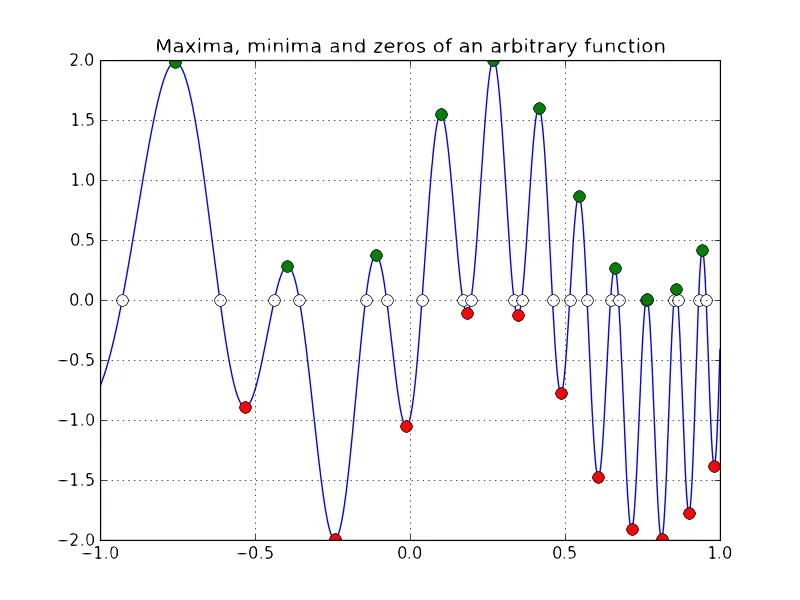
femshape
Python library for computing shape invariants of planar curves using finite element method and the FEniCS package.
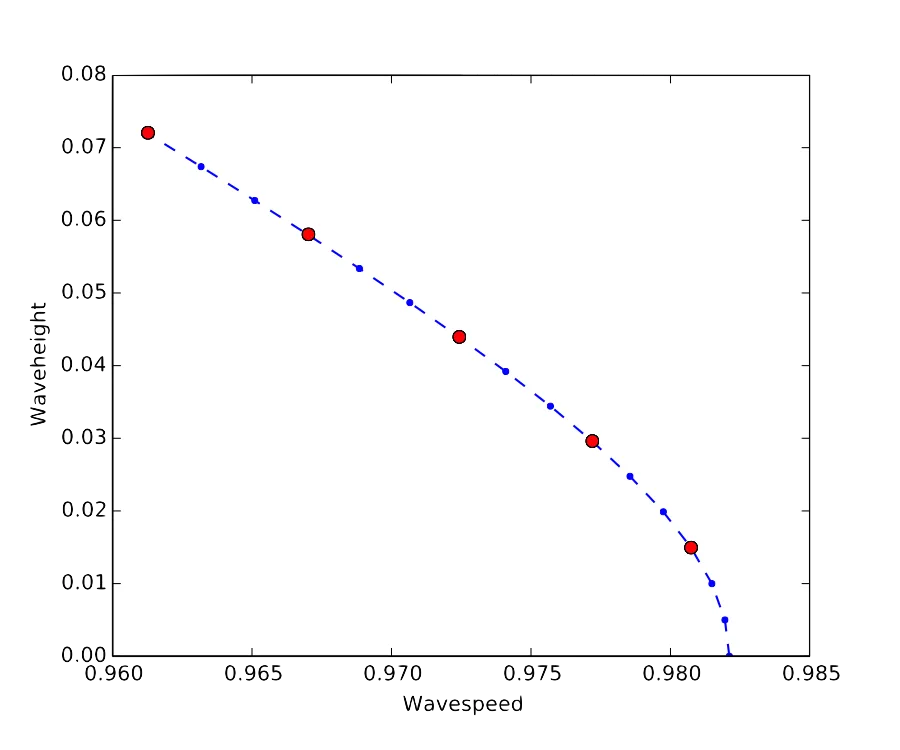
SpectraVVave
Bifurcation diagrams of traveling waves for nonlinear wave equations.
spinsys
Simulations of spin systems with the spherical midpoint method.
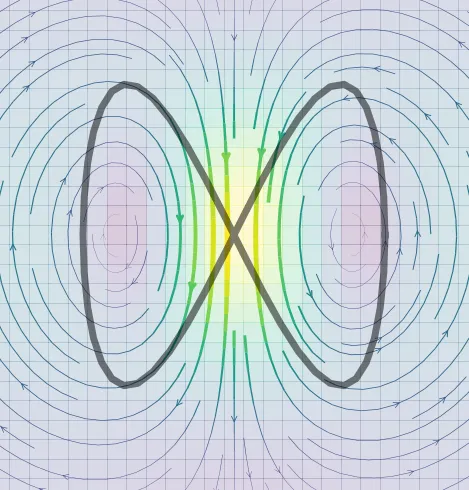
multishake
Simulations of wave maps with the multi-symplectic SHAKE method.
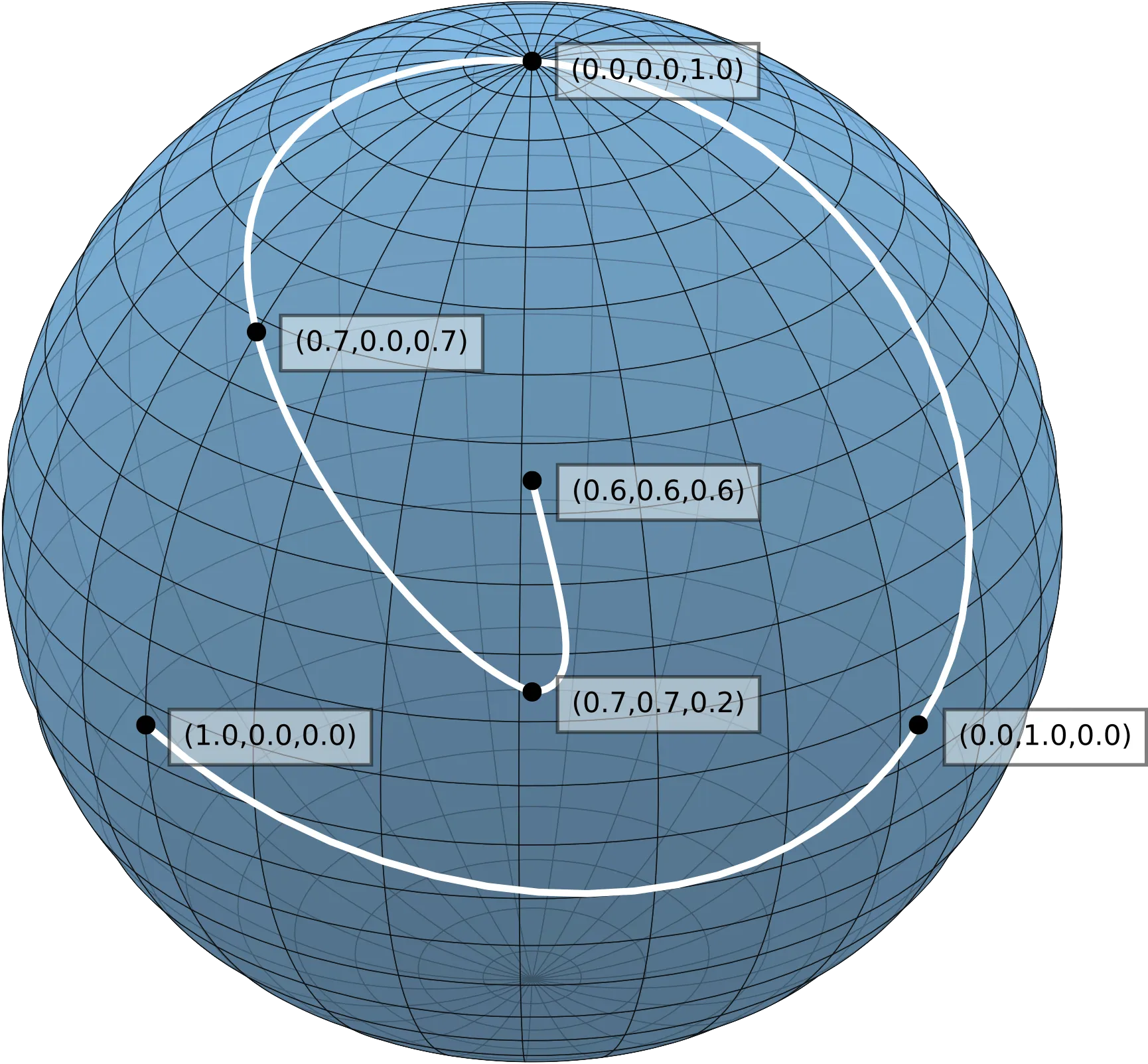
homogint
Integrate any differential equation on any homogeneous space. It is an implementation of the skeleton description of Runge–Kutta methods on homogeneous spaces. The only requirement is to have an isotropy choice at your disposal for the homogeneous space at hand. Many such isotropy choices are available from our paper. There are examples in the corresponding notebook demo.
padexp
Padé approximations of exponential (φ) functions, a port of the expint Matlab package.
odelab
Numerical simulation of ODEs in Python